Postado em 10/07/2020
Conteúdo
- Características dos Modelos Lógica Nebulosa e Perceptron multicamadas
- Conjunto de Dados
- Criando o Modelo de Treinamento
- Considerações Finais
Características dos Modelos Lógica Nebulosa e Perceptron Multicamadas
O modelo conhecido por Lógica Nebulosa, Lógica Difusa ou Lógica Fuzzy é uma extensão da lógica boolena no qual um valor lógico difuso é um valor qualquer no intervalo de valores entre 0 e 1. Os modelos que utilizam a lógica Nebulosa permitem que estados indeterminados possam ser tratados por dispositivos de controle. Desse modo, é possível avaliar conceitos não-quantificáveis tais como:
- avaliar a temperatura (quente, morno, frio, etc.)
- sentimento de felicidade(feliz, apático, triste, neutro, etc.)
- velocidade (devagar, rápido, lento, etc.)
A Lógica Nebulosa é capaz de capturar informações vagas, normalmente descritas em uma linguagem natural, convertendo-as para um formato numérico, de fácil manipulação pelos computadores atuais. Antes do surgimento da Lógica Nebulosa a manipulação de informações vagas não eram possiveis de serem processadas. Dentre suas vantagens, podemos destacar:
- Uso de variáveis liguísticas, próximas do pensamento humano;
- Requer poucas regras, valores e decisões;
- Simplifica a solução de problemas e a aquisição da base de conhecimento;
- Mais variáveis observáveis podem ser valoradas;
- Fácil de entender, manter e testar.
Como nem tudo são flores, a Lógica Nebulosa necessita de várias etapas para simulão e testes. Dependendo da base de dados, o modelo pode demorar para aprender e podem ocorrer dificuldades para estabelecer as regras corretamente. Essas dificuldades são contornadas quando existe um especialista no domínio para auxiliar na criação das regras e interpretação dos resultados.
O Perceptron Multicamadas (ou MLP - Multi Layer Perceptron) é uma rede neural que possui uma ou mais camadas ocultas e um número indeterminado de neurônios. A camada oculta possui esse nome porque não é possível prever a saída desejada que serão geradas nas camadas intermediárias. Para treinar um Perceptron Multicamadas o algoritmo normalmente utilizado é o de retropropagação (Backpropagation).
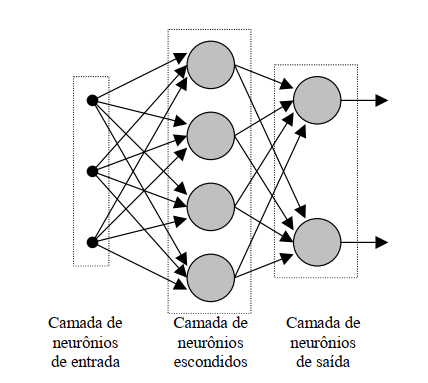
Diferentemente de outras redes neurais como o Perceptron e Adaline, onde existe apenas um único neurônio de saída Y, o Perceptron Multicamadas pode relacionar o conhecimento a vários neurônios de saída.
O algoritmo do Perceptron Multicamadas é composto de 4 etapas:
1ª Etapa: Inicialização
- Atribuir valores aleatórios para os pesos e limites
- Escolher os valores iniciais que influenciam no comportamento da rede
- Na ausência de conhecimento prévio quanto aos pesos e limites que serão utilizados, recomenda-se utilizar valores iniciais aleatórios e baixos distribuídos de forma uniforme
2ª Etapa: Ativação
- Calcular os valores dos neurônios da camada oculta
- Calcular os valores dos neurônios da camada de saída
3ª Etapa: Treinamento dos pesos
- Calcular os erros dos neurônios das camadas de saída e oculta
- Calcular a correção dos pesos
- Atualizar os pesos dos neurônios das camadas de saída e oculta
4ª Etapa: Iteração
- Repetir o processo a partir da 2ª etapa até que o critério de erro seja satisfeito
Para esse exemplo, primeiramente iremos importar as bibliotecas básicas que serão utilizadas nesse exemplo.
import numpy as np
from sklearn import datasets
from sklearn import preprocessing
import skfuzzy as fuzz
from skfuzzy import control as ctrl
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
%matplotlib inlineAlém da biblioteca NumPy, também iremos utilizar o Scikit-learn para utilizar os algoritmos de Lógica Nebulosa e Perceptron Multicamadas e a biblioteca MatPlotLib para gerar os gráficos.
Conjunto de Dados
Para esse exemplo, utilizei mais uma vez o conjunto de dados Iris. Esse conjunto possui 150 registros de 3 espécies diferentes de flor Iris: Versicolor, Setosa e Virginica. Cada registro do conjunto possui cinco características: SepalLength (Comprimento da Sépala), SepalWidth (Largura da Sépala), PetalLength (Comprimento da Pétala), PetalWidth (Largura da Pétala) e class (Classe).
Dataset disponível em: https://archive.ics.uci.edu/ml/datasets/Iris
iris = datasets.load_iris()
dados = iris.data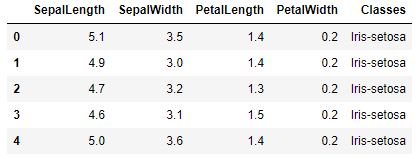
Precisamos fuzzyficar cada atributo para obter o grau de pertinencia de cada característica as classes do conjunto de dados IRIS. Para criar esse range e as faixas de pertinencia foi utilizando a transformação gaussiana.
Para normalizar as entradas executamos o passo seguinte:
preprocessar = preprocessing.MinMaxScaler()
entrada = preprocessar.fit_transform(dados)Em seguida calculamos o range, a média e o desvio padrão de cada uma das classes:
universo = np.arange(0, 1, 0.01)
media_setosa = np.mean(entrada[0:50,:])
desvio_setosa = np.std(entrada[0:50,:])
media_versicolor = np.mean(entrada[50:100,:])
desvio_versicolor = np.std(entrada[50:100,:])
media_virginica = np.mean(entrada[100:150,:])
desvio_virginica = np.std(entrada[100:150,:])Para finalmente aplicar a transformação gaussiana:
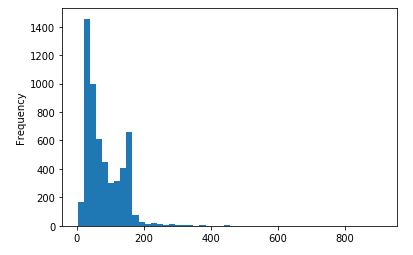
fuzzy = ctrl.Antecedent(universo, 'Lógica Nebulosa')
fuzzy['Setosa'] = fuzz.gaussmf(universo, media_setosa, desvio_setosa)
fuzzy['Versicolor'] = fuzz.gaussmf(universo, media_versicolor, desvio_versicolor)
fuzzy['Virginica'] = fuzz.gaussmf(universo, media_virginica, desvio_virginica)
fuzzy.view()
plt.show()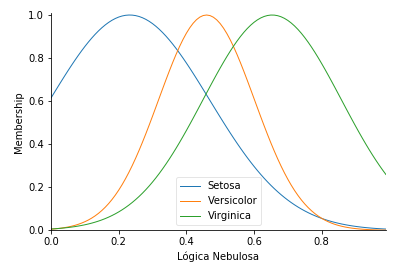
De acordo com a imagem gerada, temos a distribuição gaussiana (também conhecida por distribuição normal), em formato de uma curva simétrica em torno do seu ponto médio, apresentando assim seu famoso formato de sino. Como a base de dados é distribuída em subconjuntos de 50 isntâncias para cada classe de flor do tipo Iris, cada curva de distribuição normal representa uma das faixas de valores de uma certa probabilidade de ocorrência.
Nos próximas etapas iremos aplicar os algoritmos de Lógica Nebulosa e Perceptron Multicamadas para classificar o conjunto de dados.
Criando o Modelo de Treinamento
Para utlizar o algoritmo de Lógica Nebulosa, fuzzificar as entradas. Para isso iremos criar uma função para passar uma amostra da base de dados e, para cada atributo da amostra, iremos transformá-lo em outros 3 atributos (de acordo com o grau de pertinência para cada uma das 3 classes).
def fuzzying(vetor):
retorno = []
for i in range(len(vetor)):
retorno.append(fuzz.interp_membership(universo, fuzz.gaussmf(universo, media_setosa, desvio_setosa), vetor[i]))
retorno.append(fuzz.interp_membership(universo, fuzz.gaussmf(universo, media_versicolor, desvio_versicolor), vetor[i]))
retorno.append(fuzz.interp_membership(universo, fuzz.gaussmf(universo, media_virginica, desvio_virginica), vetor[i]))
return np.asarray(retorno).TAgora que a função está criada, vamos testá-la. Para isso iremos passar 3 valores para a função fuzzying e verificar a sua saída.
fuzzying([0.2, 0.56, 0.3, 0.8])array([0.99051683, 0.18656282, 0.08544104, 0.38156028, 0.77825999,
0.90014951, 0.95995498, 0.53004173, 0.22417374, 0.05538159,
0.0558928 , 0.77485862])
Ótimo! A função está funcionando conforme o esperado.
Agora iremos criar uma outra função para utilizar o algoritmo Perceptron Multicamadas da biblioteca do Scikit-Learn:
def gerar_mlp(neuronios, taxa_aprendizado, max_iteracoes):
mlp = MLPRegressor(
solver='adam',
hidden_layer_sizes=(neuronios,),
random_state=1,
learning_rate='constant',
learning_rate_init=taxa_aprendizado,
max_iter=max_iteracoes,
activation='logistic',
momentum=0.1
)
return mlpUtilizando a função de fuzzificação, iremos processar todo o conjunto de dados da Iris:
entradas_fuzzy = []
for i in range(150):
entradas_fuzzy.append(fuzzying(entrada[i,:]))
entradas_fuzzy = np.asarray(entradas_fuzzy)
entradas_fuzzyE transforma os vetores de saída para o tipo de dado float, mudando de [-1,0,1] em [0,0.5,1]:
saida = np.arange(150, dtype=float)
for i in range(150):
if i <50:
saida[i] = 0
if 50 <= i < 100:
saida[i] = 0.5
if 100 <= i < 150:
saida[i] = 1
saida = saida.reshape(150,1)Em seguida, como o objetivo é que a saída da Perceptron Multicamadas seja um valor processado pela Lógica Nebulosa, uma vez que teremos um único neurônio na camada de saida (dando uma resposta numérica, assim como uma regressão), precisamos criar uma função para indicar as faixas de resposta para cada uma das classes:
def obter_classe(respostas, valor_menor, valor_maior):
label_previsto = []
for i in respostas:
if i < valor_menor:
label_previsto.append('Setosa')
elif i >= valor_menor and i <= valor_maior:
label_previsto.append('Versicolor')
else:
label_previsto.append('Virginica')
return label_previstoOutro passo importante é criar uma última função para mudar as saídas de [0,0.5,1] para [‘Setosa’, ‘Versicolor’, ‘Virginica’]:
def traduz_saida(saidas):
resposta = []
for i in saidas:
if i == 0:
resposta.append('Setosa')
elif i == 0.5:
resposta.append('Versicolor')
else:
resposta.append('Virginica')
return respostaFinalmente, depois de tantas funções e transformações, podemos aplicaar o algoritmo Perceptron Multicamadas utilizando uma validação cruzada de tamanho três e gerando um relatório de desempenho para cada uma das interações:
skf = StratifiedShuffleSplit(n_splits=3, test_size=0.25)
for train_idx, test_idx in skf.split(entradas_fuzzy,saida.ravel()):
x_treinamento = entradas_fuzzy[train_idx]
y_treinamento = saida[train_idx]
x_teste = entradas_fuzzy[test_idx]
y_teste = saida[test_idx]
mlp = gerar_mlp(20, 0.01, 100)
mlp.fit(x_treinamento, y_treinamento.ravel())
previsao = obter_classe(mlp.predict(x_teste), 0.25, 0.8)
print('######################################################')
print(classification_report(traduz_saida(y_teste), previsao))A saída gerada será algo semelhante com o relatório a seguir:
######################################################
precision recall f1-score support
Setosa 1.00 1.00 1.00 13
Versicolor 0.83 0.83 0.83 12
Virginica 0.85 0.85 0.85 13
accuracy 0.89 38
macro avg 0.89 0.89 0.89 38
weighted avg 0.89 0.89 0.89 38
######################################################
precision recall f1-score support
Setosa 0.92 0.92 0.92 12
Versicolor 0.85 0.85 0.85 13
Virginica 0.92 0.92 0.92 13
accuracy 0.89 38
macro avg 0.90 0.90 0.90 38
weighted avg 0.89 0.89 0.89 38
######################################################
precision recall f1-score support
Setosa 0.92 0.92 0.92 12
Versicolor 0.86 0.92 0.89 13
Virginica 1.00 0.92 0.96 13
accuracy 0.92 38
macro avg 0.92 0.92 0.92 38
weighted avg 0.92 0.92 0.92 38
Utilizando a Lógica Nebulosa com o algoritmo Perceptron Multicamadas foi obtido uma precisão entre 89% e 92%. Um resultado que considero muito bom para esse conjunto de dados.
Considerações Finais
Mais uma vez utilizamos o conjunto de dados de flores Iris para apresentar outros dois importantes modelos de aprendizagem de máquina bastante utilizado pelos Cientistas de Dados. Obtivemos um resultado entre 89% e 92% de precisão. Como sempre, recomenda-se conhecer o funcionamento e características desses modelos para tirar proveitos das suas vantagens e conhecer as suas limitações. Mesmo com tantas etapas de transformação dos dados e fuzzificação, a Lógica Nebulosa é muito aplicada e apresenta uma série de vantagens, conforme apresentado na sua descrição.
Como sempre sugiro, você também pode aplicar esse modelo em outras bases disponibilizadas na Internet, bastando fazer alguns ajustes quando necessário. Todo o código e mais um pouco está disponível no meu GitHub.
Os passos de execução deste tutorial foram testados com Python 3.6 e tudo ocorreu sem problemas. No entanto, é possível que alguém encontre alguma dificuldade ou erro no meio do caminho. Se for o caso, por favor comente a sua dificuldade ou erro neste post.