Postado em 16/07/2020

Conteúdo

1. Características do Algoritmo PCA
2. Conjunto de Dados
3. Criando o Modelo de Treinamento
4. Considerações Finais

Características do Algoritmo PCA

O algoritmo de Análise de Componentes Principais (Principal Component Analysis, ou somente PCA) é uma modelo de aprendizagem de máquina não supervisionado utilizado para tentar reduzir a dimensionalidade (número de recursos) de um conjunto de dados, tentando, ainda, manter o maior número possível de informações. É um dos métodos multivariado mais utilizados e conhecido para a redução de dados.

O algoritmo usa um conjunto de recursos representado por uma matriz de N registros por P atributos, que podem estar correlacionados entre si, e sumariza esse conjunto por eixos não correlacionados (componentes principais) que são uma combinação linear das P variáveis originais. O primeiro componente represente a maior variabilidade possível nos dados, o segundo componente, a segunda maior variabilidade, e assim por diante.

O algoritmo PCA usa a distância euclidiana calculada a partir dos P atributos como uma medida de dissimilaridade entre os N objetos. Para isso, o algoritmo PCA calcula as K melhores possíveis dimensões (K < P) representandos a distância euclidiana entre os objetos.

Para esse exemplo, primeiramente iremos importar as bibliotecas básicas que serão utilizadas nesse exemplo.

from numpy import *
from pylab import *

Além da biblioteca NumPy, também iremos utilizar a biblioteca PyLab que permite gerar gráficos de duas dimensões de excelente qualidade, permitindo edição interativa, animações, inúmeros tipos de gráficos diferentes e o salvamento das imagens geradas em diversos formatos diferentes.

Conjunto de Dados

Para esse exemplo, mais uma vez foi utilizado o conjunto de dados Iris. Esse conjunto possui 150 registros de 3 espécies diferentes de flor Iris: Versicolor, Setosa e Virginica. Cada registro do conjunto possui cinco características: SepalLength (Comprimento da Sépala), SepalWidth (Largura da Sépala), PetalLength (Comprimento da Pétala), PetalWidth (Largura da Pétala) e class (Classe).

Dataset disponível em: https://archive.ics.uci.edu/ml/datasets/Iris

f = open("iris.csv","r")
setosa = []
versicolor = []
virginicia = []

Já aproveitamos para criar os dataframes com as classes de flores iris presentes no conjunto de dados. Desse modo, já deixamos tudo preparado para os próximos passos.

for data in f.readlines():
    val = data.split(",")
    iris_type = val[-1].rsplit()[0]
    values = [double(i) for i in val[:-1]]    
    if(iris_type == "Iris-setosa"):
        setosa.append(values) 
    if(iris_type == "Iris-versicolor"):
        versicolor.append(values)
    if(iris_type == "Iris-virginicia"):
        virginicia.append(values)

Criando o Modelo de Treinamento

Dessa vez optamos por criar o códido do algoritmo PCA do zero, sem utilizar nenhuma biblioteca. Para isso, definimos a função a seguir:

def pca(X,reduced_dimension=None):

    samples,dim = X.shape    
    
    X = (X-X.mean(axis = 0))/(X.var(axis=0))**(1/2.0)  
    
    U,S,V = linalg.svd(X)       

    if reduced_dimension:
        V = V[:reduced_dimension]
    return V.T

No algoritmo PCA, os objetos são representados por uma nuvem de N pontos em um espaço multidimensional, com um eixo para cada uma dos P atributos, de modo que:

• o centroide dos pontos é definido pela média de cada atributo; e
• a variância de cada atributo é média dos quadrados da diferença dos N pontos com relação a média de cada atributo.

Desse modo, a fórmula geométrica do PCA é:

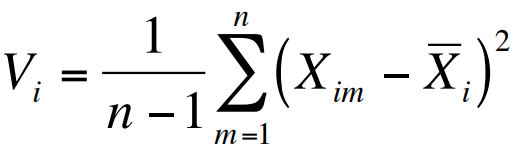
O passo seguinte é computar a matriz de projeção dos componentes principais utilizando a função PCA para cada uma das classe. O número 2 que foi atribuído significa que queremos que nossa matriz de projeção seja projetada em duas dimensões.

setosa_pc_projection_matrix = pca(array(setosa),2)
versicolor_pc_projection_matrix =  pca(array(versicolor),2)
virginicia_pc_projection_matrix =  pca(array(virginicia),2) 

low_dim_setosa_points = dot(array(setosa),setosa_pc_projection_matrix)
low_dim_versicolor_points = dot(array(versicolor),versicolor_pc_projection_matrix)
low_dim_virginicia_points = dot(array(virginicia),virginicia_pc_projection_matrix)

Pronto! Os componentes principais foram projetados. Agora vamos plotar os dados para verificar o resultado.

p1 = plot(low_dim_setosa_points[:,0].tolist(),low_dim_setosa_points[:,1].tolist(),"ro", label="Iris Setosa", color='green')
p2 = plot(low_dim_versicolor_points[:,0].tolist(),low_dim_versicolor_points[:,1].tolist(),"r*",label="Iris versicolor", color='red')
p3 = plot(virginicia_pc_projection_matrix[:,0].tolist(),virginicia_pc_projection_matrix[:,1].tolist(),"r^",label="Iris virginicia", color='blue')

title("Redução de Dimensionalidade com PCA")
xlabel("X1")
ylabel("X2") 
legend(loc = "lower right")
show()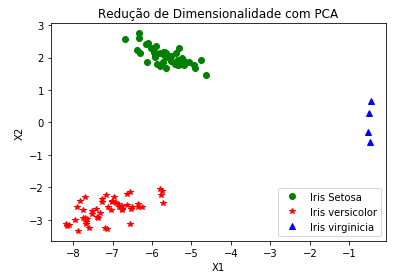

Considerações Finais

Na prática, os algoritmo PCA não é utilizado em conjunto de dados com pouicas variáveis. Precisa ter, pelo menos 3 ou mais dimensões para que ele possa ser aplicado. Outro ponto importante sobre o algoritmo PCA é que ele funciona melhor quando as variáveis estão representadas na mesma unidade. Caso contrário, as variáveis com alta variância irão dominar os componentes principais. Para evitar esse problema, recomenda-se normalizar os atributos.

Fica mais uma vez a dica de aplicar esse modelo em outras bases disponibilizadas na Internet, bastando fazer alguns ajustes caso seja necessário. Todo o código e mais um pouco está disponível no meu GitHub.

Os passos de execução deste tutorial foram testados com Python 3.6 e tudo ocorreu sem problemas. No entanto, é possível que alguém encontre alguma dificuldade ou erro no meio do caminho. Se for o caso, por favor comente a sua dificuldade ou erro neste post.